第一章　空间向量与立体几何

1.1 空间向量及其运算

1.1.1 空间向量及其线性运算

• 在空间，我们把具有大小和方向的量叫做空间向量（space vector）
  空间向量的大小叫做空间向量的长度或模（modulus）
  空间向量用黑体字母 a，b，c，... 表示，书写用 $\overrightarrow{a}$
• 空间向量用有向线段表示，向量 a 也记作 $\overrightarrow{AB}$，其模记为 |a| 或 $|\overrightarrow{a}|$
• 我们规定，长度为 0 的向量叫做零向量（zero vector），记为 0
  模为 1 的向量叫做单位向量（unit vector）
  与向量 a 长度相等而方向相反的向量，叫做 a 的相反向量，记为 -a
• 如果表示若干空间向量的有向线段所在的直线互相平行或重合，那么这些向量叫做共线向量（collinear vectors）或平行向量（parallel vectors）。
  我们规定：零向量与任意向量平行。
• 方向相同且模相等的向量叫做相等向量（equal vectors）
• 任意两个空间向量都可以平移到同一个平面内，成为同一平面内的两个向量。

• 定义空间向量的加法、减法以及数乘运算：
  

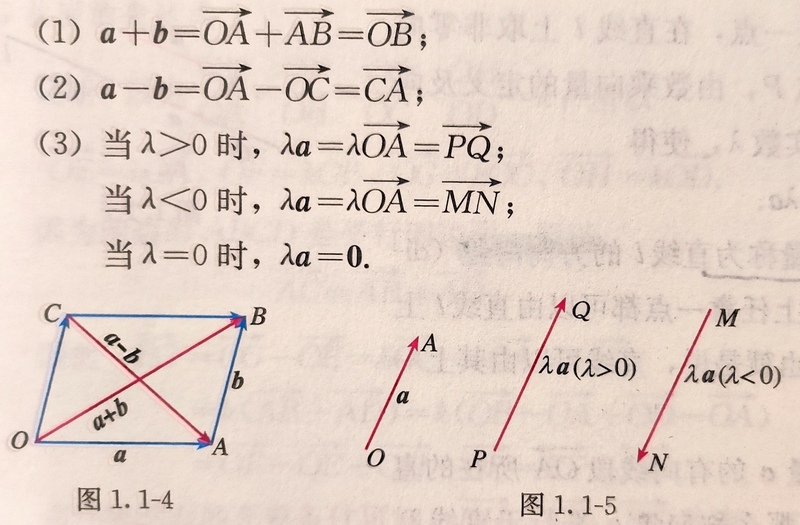
• 空间向量的线性运算满足以下运算律（其中$λ，μ\in R$）：
  交换律：a + b = b + a
  结合律：（a+b）+c = a+（b+c），λ(μa) = (λμ)a
  分配律：(λ+μ)a = λa+μa，λ(a+b) = λa+λb
• 有限个向量求和，交换相加向量的顺序，其和不变。
• 一般地，对于三个不共面的向量 a，b，c，以任意点 O 为起点，a，b，c 为邻边作平行六面体，则 a，b，c 的和等于以 O 为起点的平行六面体对角线所表示的向量。
• 对任意两个空间向量 a，b（b ≠ 0），a//b 的充要条件是存在实数 λ，使 a = λb
• 我们把与向量 a 平行的非零向量称为直线 l 的方向向量（direction vector）
  直线可以由其上一点和它的方向向量确定。
• 平行于同一个平面的向量，叫做共面向量（coplanar vectors）
• 如果两个向量 a，b 不共线，那么向量 p 与向量 a，b 共面的充要条件是存在唯一的有序实数对（x，y），使 p = xa + yb

1.1.2 空间向量的数量积运算

• 已知两个非零向量 a，b，在空间任取一点 O，作$\overrightarrow{OA}=\textbf{a}$，$\overrightarrow{OB}=\textbf{b}$，则 $\angle AOB$ 叫做向量 a，b 的夹角，记作 $<\textbf{a},\textbf{b}>$
  通常规定，$0\leqslant <\textbf{a},\textbf{b}>\leqslant \pi$，且 $<\textbf{a},\textbf{b}> = <\textbf{b},\textbf{a}>$
• 如果 $<\textbf{a},\textbf{b}>=\frac{\pi}{2}$，那么向量 a，b互相垂直，记作 $\textbf{a}\perp \textbf{b}$
• 已知两个非零向量 a，b，则 $|\textbf{a}||\textbf{b}|cos<\textbf{a},\textbf{b}>$ 叫做 a，b 的数量积（inner product），记作 $\textbf{a}\bullet \textbf{b}$
  特别地，零向量与任意向量的数量积为 0
  $\textbf{a}\perp\textbf{b}\Leftrightarrow\textbf{a}\bullet\textbf{b}=0$
  $\textbf{a}\bullet\textbf{a}=|\textbf{a}||\textbf{a}|cos<\textbf{a},\textbf{a}>=|\textbf{a}|^2$
• 空间中向量对向量的投影，可以先将它们平移到同一个平面内，利用平面上向量的投影来计算
• 空间向量的数量积满足以下的运算律：
  $(\lambda\textbf{a})\bullet\textbf{b} =\lambda(\textbf{a}\bullet\textbf{b}),\lambda\in R$
  $\textbf{a}\bullet\textbf{b} =\textbf{b}\bullet\textbf{a}$ 交换律
  $(\textbf{a}+\textbf{b})\bullet\textbf{c} =\textbf{a}\bullet\textbf{c}+\textbf{b}\bullet\textbf{c}$ 分配律

1.2 空间向量基本定理

• 定理 如果三个向量 a，b，c 不共面，那么对任意一个空间向量 p，存在唯一的有序实数组（x，y，z），使得 p=xa+yb+zc
• 空间任意三个不共面的向量都可以构成空间的一个基底（base）。
  特别地，如果空间的一个基底中的三个基向量两两垂直，且长度都为 1，那么这个基底叫做单位正交基底，常用 {i，j，k} 表示。
• 把一个空间向量分解为三个两两垂直的向量，叫做把空间向量进行正交分解。

1.3 空间向量及其运算的坐标表示

1.3.1 空间直角坐标系

• 右手直角坐标系
• 在单位正交基底下与向量对应的有序实数组叫做该点在空间直角坐标系中的坐标，记作 A（x，y，z），其中 x 叫做点 A 的横坐标，y 叫做点 A 的纵坐标，z 叫做点 A 的竖坐标。
• 向量 a 在空间直角坐标系中的坐标，简记作 a=（x，y，z）
• 在空间直角坐标系中，空间中的点和向量都可以用三个有序实数表示。

1.3.2 空间向量运算的坐标表示

• 设 $\textbf{a}=(a_1,a_2,a_3),\textbf{b}=(b_1,b_2,b_3)$，我们有：
  $\textbf{a+b}=(a_1+b_1,a_2+b_2,a_3+b_3)$，
  $\textbf{a-b}=(a_1-b_1,a_2-b_2,a_3-b_3)$
  $\lambda\textbf{a}=(\lambda a_1,\lambda a_2,\lambda a_3),\lambda\in R$
  $\textbf{a}\bullet\textbf{b}=a_1b_1+a_2b_2+a_3b_3$
• 空间向量运算的坐标表示与平面向量运算的坐标表示是完全一致的。
• 一个空间向量的坐标等于表示此向量的有向线段的终点坐标减去起点坐标。
• 当 b ≠ 0 时，$\textbf{a}//\textbf{b}\Leftrightarrow\textbf{a}=\lambda\textbf{b}\Leftrightarrow a_1=\lambda b_1,a_2=\lambda b_2,a_3=\lambda b_3(\lambda\in R)$
  $\textbf{a}\perp\textbf{b}\Leftrightarrow\textbf{a}\bullet\textbf{b}=0\Leftrightarrow a_1b_1+a_2b_2+a_3b_3=0$
  $|\textbf{a}|=\sqrt{\textbf{a}\bullet\textbf{a}}=\sqrt{a_1^2+a_2^2+a_3^2}$
  $cos<\textbf{a},\textbf{b}>=\frac{\textbf{a}\bullet\textbf{b}}{|\textbf{a}||\textbf{b}|}=\frac{a_1b_1+a_2b_2+a_3b_3}{\sqrt{a_1^2+a_2^2+a_3^2}\sqrt{b_1^2+b_2^2+b_3^2}}$
• 空间两点间的距离公式：
  $P_1P_2=|\overrightarrow{P_1P_2}|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}$
• 向量概念的推广和应用：一般地，n 元有序实数组（a1，a2，...，an）称为 n 维向量，它是几何向量的推广。n 维向量的全体构成的集合，赋予相应的结构后，叫做 n 维向量空间。它的每一个元素可看成 n 维向量空间的一点。

1.4 空间向量的应用

1.4.1 用空间向量研究直线、平面的位置关系
1.空间中点、直线和平面的向量表示

• 空间任意直线由直线上一点及直线的方向向量唯一确定
• 空间中任意平面由空间一点及两个不共线向量唯一确定
• 平面的法向量

2.空间中直线、平面的平行

• 直线的方向向量和平面的法向量是确定空间中的直线和平面的关键量。
• 如果两条直线平行，那么它们的方向向量一定平行；反过来，如果两条直线的方向向量平行，那么这两条直线也平行。
• 两个平面的法向量平行，则这两个平面平行；反之亦然。
• 直线平行于平面，则这条直线与平面的法向量垂直；反之亦然。
• 平面与平面平行的判定定理：若一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。
• 直线与平面平行的判定定理：若平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

3.空间中直线、平面的垂直

• 一般地，直线与直线垂直，就是两直线的方向向量垂直；直线与平面垂直，就是直线的方向向量与平面的法向量平行；平面与平面垂直，就是两平面的法向量垂直。
• 平面与平面垂直的判定定理：若一个平面过另一个平面的垂线，则这两个平面垂直。

1.4.2 用空间向量研究距离、夹角问题

• 直线外一点到直线的距离：投影向量、勾股定理
• 一般地，两条异面直线所成的角，可以转化为两条异面直线的方向向量的夹角来求得。
• 直线与平面所成的角，可以转化为直线的方向向量与平面的法向量的夹角。
• 两个平面相交，形成四个二面角，我们把这四个二面角中不大于90度的二面角称为两个平面的夹角。
• 解决立体几何中的问题，可用三种方法：综合法、向量法、坐标法。综合法以逻辑推理作为工具解决问题；向量法利用向量的概念及其运算解决问题；坐标法利用数及其运算来解决问题。

第二章　直线和圆的方程

2.1 直线的倾斜角与斜率

2.1.1 倾斜角与斜率

• 当直线 l 与 x 轴相交时，我们以 x 轴为基准，x 轴正向与直线 l 向上的方向之间所成的角 α 叫做直线 l 的倾斜角（angle of inclination）
• 当直线 l 与 x 轴平行或重合时，我们规定它的倾斜角为 0°，因此，直线的倾斜角 α 的取值范围为 0°≤ α < 180°
• 直线 l 的倾斜角 α 与直线 l 上的两点$P_1(x_1,y_1),P_2(x_2,y_2)(x_1\neq x_2)$ 的坐标有如下关系：
  $tan \alpha =\frac{y_2-y_1}{x_2-x_1}$
• 我们把一条直线的倾斜角 α 的正切值叫做这条直线的斜率（slope），常用小写字母 k 表示。
• 倾斜角是 90° 的直线没有斜率，倾斜角不是 90° 的直线都有斜率。

2.1.2 两条直线平行和垂直的判定

• 两条直线平行，斜率相等；两条直线斜率相等，两直线平行。
• 如果两条直线都有斜率，且它们互相垂直，那么它们的斜率之积等于 -1；反之亦然。

2.2 直线的方程

2.2.1 直线的点斜式方程

• 方程 $y-y_0=k(x-x_0)$ 由直线上一个定点 $(x_0,y_0)$ 及该直线的斜率 k 确定，我们把它叫做直线的点斜式方程，简称点斜式（point slope form）
• 当直线 l 的倾斜角为 0° 时，直线 l 的方程是 $y=y_0$
• 当直线 l 的倾斜角为 90° 时，直线没有斜率，它的方程为 $x=x_0$
• 我们把方程 y=kx+b 叫做直线的斜截式方程，简称斜截式（slope intercept form），其中 k 是直线的斜率，b 是直线在 y 轴上的截距。

2.2.2 直线的两点式方程

• 经过两点 $P_1(x_1,y_1),P_2(x_2,y_2)(其中 x_1\neq x_2,y_1\neq y_2)$ 的直线的方程，我们把它叫做直线的两点式方程，简称两点式（two-point form）
  $\frac{y-y_1}{y_2-y_1} = \frac{x-x_1}{x_2-x_1}$
• 方程 $\frac{x}{a}+\frac{y}{b}=1$ 由直线 l 在两条坐标轴上的截距 a 与 b 确定，我们把方程 $\frac{x}{a}+\frac{y}{b}=1$ 叫做直线的截距式方程，简称截距式（intercept form）

2.2.3 直线的一般式方程

• 我们把关于 x，y 的二元一次方程 Ax+By+C=0 （其中 A，B 不同时为 0）叫做直线的一般式方程，简称一般式（general form）

2.3 直线的交点坐标与距离公式

2.3.1 两条直线的交点坐标

• 两条直线的交点坐标也就是两条直线的方程所组成的方程组的解。

2.3.2 两点间的距离公式

• $P_1(x_1,y_1),P_2(x_2,y_2)$ 两点间的距离公式：
  $|P_1P_2|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

2.3.3 点到直线的距离公式

• 点$P(x_0,y_0)$到直线 l：Ax+By+C=0 的距离
  $d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}$

2.3.4 两条平行直线间的距离

• 两条平行直线 $Ax+By+C_1=0 与 Ax+By+C_2=0$ 间的距离为
  $d=\frac{|C_1-C_2|}{\sqrt{A^2+B^2}}$

2.4 圆的方程

2.4.1 圆的标准方程

• 圆心为 A（a，b），半径为 r 的圆的标准方程（standard equation of circle）
  $(x-a)^2+(y-b)^2=r^2$
• 不在同一条直线上的三个点可以确定一个圆，三角形有唯一的外接圆。
• 三角形外接圆的圆心是三角形的外心，即三角形三边垂直平分线的交点。

2.4.2 圆的一般方程

• 一般地，圆的标准方程可以变形为$x^2+y^2+Dx+Ey+F=0$的形式：
  （1）当$D^2+E^2-4F>0$时，上述方程表示一个圆，我们把它叫做圆的一般方程（general equation of circle）
  （2）当$D^2+E^2-4F=0$时，方程只有实数解，它表示一个点；
  （3）当$D^2+E^2-4F<0$时，方程没有实数解，它不表示任何图形。

2.5 直线与圆、圆与圆的位置关系

2.5.1 直线与圆的位置关系

• 直线与圆的位置关系：
  （1）直线与圆相交，有两个公共点；
  （2）直线与圆相切，只有一个公共点；
  （3）直线与圆相离，没有公共点。
• 判断直线与圆的方程组有无实数解、有几个实数解，来判断两者的位置关系
• 依据圆心到直线的距离与半径的关系，判断直线与圆的位置关系

2.5.2 圆与圆的位置关系

• 两个圆之间存在以下三种位置关系：
  （1）两圆相交，有两个公共点；
  （2）两圆相切，包括外切与内切，只有一个公共点；
  （3）两圆相离，包括外离与内含，没有公共点。
• 两圆的方程组的实数解的个数确定两圆位置关系
• 依据两圆的圆心距与两半径的和或两半径的差的绝对值的大小关系，判断两圆的位置关系。

第三章 圆锥曲线的方程